Binär oder Text - das ist hier die Frage
Published on Friday, June 6, 2014 4:00:00 AM UTC in
Programming

Wenn man wissen möchte, ob eine Datei Text oder Binärdaten enthält, sieht man sich die Dateiendung an. Was aber, wenn es keine Dateiendung gibt oder man diese nicht kennt? Als Mensch hat man es einfach, weil unser Gehirn Erstaunliches leistet. Eine Entscheidung kostet nur einen kurzen Blick auf den Inhalt einer Datei, um erkennen zu können, ob er als Text Sinn ergibt oder aussieht wie ein Teller Spaghetti. Ein Computer hat es da schon deutlich schwerer, und mit ihm der Programmierer. Was tun?
Die grundsätzliche Idee
Auf der Suche nach Lösungen stolperte ich zunächst über einige naive Ansätze wie etwa "prüfe einfach, ob Byte-Werte > 128 vorhanden sind", "die Datei darf keine Null-Werte enthalten", oder auch "splitte nach Leerzeichen und stelle sicher, dass keine Wörter mit mehr als X Zeichen vorhanden sind". All diese Vorschläge funktionieren nur mit trivialen Beispielen. Tatsächlich gibt es sehr viele Textdateien, in denen legitime Byte-Werte > 128 enthalten sind (siehe unten), Null-Werte sind sogar eher die Regel, wenn man bestimmte Unicode-Varianten betrachtet, und bestimmte Formate wie RTF haben teils endlose Buchstabenketten ohne ein Leerzeichen, so dass spätestens dann auch eine "Wortlängenprüfung" nicht mehr klappt.
Irgendwann stieß ich auf den Hinweis, dass man vielleicht eine statistische Analyse mit Markow-Ketten machen könnte, um das Problem zu lösen. Das klang interessant, aber viel mehr als diesen Hinweis findet man kaum, da sich die meisten Treffer zu dem Thema in Zusammenhang mit Text und Textdateien eher mit der Generierung von (natürlich-sprachlich klingendem) Text statt mit der Analyze beschäftigen. Also habe ich mich daran gemacht, selbst eine robuste Lösung zu bauen.
Die diversen Feinheiten und Ausprägungen von Markow-Ketten auszuführen würde vollständig den Rahmen dieses Artikels sprengen, aber Wikipedia hilft jenen gerne weiter, die die (mathematischen) Details wissen möchten. Für unseren Anwendungsfall muss man nur folgende Eckdaten nutzen:
- Wir betrachten ein System als die Menge seiner möglichen Zustände
- Insbesondere interessieren uns die Wahrscheinlichkeiten, mit denen das System von einem Zustand in einen beliebigen anderen übergeht
Weitere Details, insbesondere die Abhängigkeiten oder Bedingungen von Zustandsübergängen, sind für uns irrelevant, da wir keine auf Markow-Ketten aufbauenden, komplexeren Modelle oder Analysen verwenden müssen. Das macht die Sache recht einfach, auch wenn es vielleicht noch nicht so aussieht.
Wer das Wort "Zustandsübergang" hört, denkt vermutlich gleich an einen zeitlichen Ablauf. Tatsächlich treffen Markow-Ketten aber keine Aussage darüber, ob Übergänge etwas mit Zeit zu tun haben. In unserem Beispiel sind die Zustände die möglichen Byte-Werte einer Datei, und die Zustandsübergänge einfach der Sprung zum jeweils nachfolgenden Byte-Wert. Dabei interessiert uns, wie wahrscheinlich es ist, dass auf einen bestimmten Byte-Wert A ein bestimmter anderer Byte-Wert B folgen wird. Um solche Wahrscheinlichkeiten zu lernen, trainiert man das System vor dem Einsatz mit bekannten Beispielen (= Beispieldateien, von denen man sicher weiß, dass sie Text enthalten). Es handelt sich bei dem Ansatz also um eine Form des Maschinenlernens.
Eine einfache Implementierung
Zur Ablage der Wahrscheinlichkeiten reicht ein zweidimensionales Array mit der Länge [256,256] aus, um eine Matrix aller möglichen Zustandsübergänge aller möglichen Byte-Werte zu bauen. Eine simple Implementierung kann zur Analyse einfach eine Menge von Bytes (zum Beispiel einen absichtlich als Binäredaten gelesenen Datei-Inhalt) Schritt für Schritt durchlaufen, und für den Übergang vom einen zum nächsten Byte zunächst stumpfsinnig die Anzahl aufsummieren. Etwa so:
private readonly double[,] _probabilities = new double[256, 256];
public void Analyze(byte[] rawData)
{
if (rawData.Length < 2)
{
return;
}
for (var n = 0; n < rawData.Length - 1; n++)
{
var current = rawData[n];
var next = rawData[n + 1];
_probabilities[current, next] += 1.0;
}
}
Diesen Schritt kann man beliebig oft durchführen (= für eine beliebige Anzahl von Dateiinhalten) und hat dann am Ende eine nicht-normalisierte absolute Menge für die Zustandsübergänge seiner Beispieldaten. Damit man sie im Sinne von Markow nutzen kann, muss man eine Normalisierung durchführen, d.h. sicherstellen, dass die Summe jeder Zeile genau 1 ergibt (oder 0, falls kein einziger Zustandsübergang für den Byte-Wert registriert wurde). Also etwa:
public double[,] GetProbabilities()
{
var lengthX = _probabilities.GetLength(0);
var lengthY = _probabilities.GetLength(1);
var result = new double[lengthX, lengthY];
for (var i = 0; i < lengthX; i++)
{
var sum = 0.0;
for (var j = 0; j < lengthY; j++)
{
sum += _probabilities[i, j];
}
if (sum <= double.Epsilon)
{
continue;
}
for (var j = 0; j < lengthY; j++)
{
result[i, j] /= sum;
}
}
return result;
}
Damit ist der erste Schritt, die Analyse, schon abgeschlossen.
Ein Blick auf die Daten
Bevor man die Daten verwendet, lohnt sich ein genauerer Blick darauf. Ich habe zum Test etwa 12000 C#-Dateien eingelesen und derart auswerten lassen. Natürlich hätte ich jede andere Art von Text, auch gut gemischt, verwenden können – was bei realer Anwendung auch sehr sinnvoll gewesen wäre. Ich möchte aber im späteren Verlauf noch etwas demonstrieren :-), weshalb ich mich an dieser Stelle bewusst künstlich auf C#-Dateien beschränkt habe. Für diese Dateien sieht die Analyse, ausgegeben als Diagramm, etwa so aus (zum Vergrößern klicken):

Wie man sieht, spielt sich die Hauptsache tatsächlich zwischen den Byte-Werten 32 (Leerzeichen) und 125 (geschweifte Klammer zu) ab. Man sieht aber auch, dass außerhalb dieses Bereichs durchaus einige Aktivität zu erkennen ist. Für eine genauere Betrachtung sind auf jeden Fall immer die Extremwerte interessant, beispielsweise dieser Bereich:
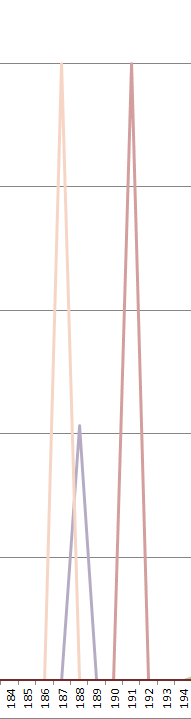
Was bedeutet das? Die linke Spitze (heller) gehört zur Datenreihe 239, die rechte (dunkler) zur Reihe 187. Der Ausschlag geht jeweils bis zum Y-Wert 1.0. Was diese Spitzen aussagen ist:
- Auf einen Byte-Wert von 239 folgt immer ein Byte-Wert von 187.
- Auf einen Byte-Wert von 187 folgt immer ein Byte-Wert von 191.
Oder anders formuliert: wenn es in einer (egal welcher) meiner C#-Dateien das Byte 239 gibt, dann leitet sie immer die Werte-Folge 239, 187, 191 ein, nie eine andere. Wer sich ein wenig mit Encodings auskennt weiß, dass diese Bytes das sogenannte Byte Order Mark für UTF-8 darstellen. Sprich: mindestens eine meiner C#-Dateien ist UTF-8-kodiert, vermutlich sogar der überwiegende Teil davon.
Ein zweites Byte Order Mark ist ganz am Ende des Diagramms zu erkennen, wo man ablesen kann, das auf den Wert 255 immer 254 folgt. Zumindest eine der Dateien scheint also in UTF-16 kodiert zu sein.
Man kann aber auch Plattformspezifisches ablesen:

Die rote Spitze (Datenreihe 13) erzählt, dass auf den Wert 13 immer ein Wert 10 folgt. Hierbei handelt es sich um einen Zeilenumbruch, der unter Windows eben per CR LF ausgedrückt wird. Hätte ich meine Dateien unter Linux geschrieben gäbe es diesen Zusammenhang so vielleicht nicht, da dort Zeilenumbrüche nur durch LF (Wert 10) ausgedrückt werden.
Auch die Eigenheiten der Programmiersprache kann man ablesen, etwa dass auf diverse Zeichen wie geschweifte Klammern oder das Semikolon mit sehr hoher Wahrscheinlichkeit ein Zeilenumbruch folgt.
Und schließlich werden sogar persönliche Vorlieben preisgegeben, wenn man genauer hinsieht. Beispielsweise folgt mit fast 60-prozentiger Wahrscheinlichkeit auf ein Leerzeichen (32) ein weiteres Leerzeichen – ein Hinweis darauf, dass für die Einrückung von Code Leerzeichen statt Tabs verwendet wurden.
Weiter zur Auswertung
Mit diesen Daten bewaffnet kann man sich nun an der Auswertung versuchen. Mir war zunächst überhaupt nicht bewusst, wie eine sinnvolle Bewertung von (unbekannten) Daten an Hand der obigen Verteilungswerte aussehen kann, und so habe ich recht lange mit unterschiedlichsten Verfahren herumgespielt: Summierung von Fehlerquadraten, Standardabweichung, diverse Gewichtungen von Ausreißern und ähnlichem – alles mit zwar tendenziell richtigen, aber trotzdem recht unbefriedigenden Ergebnissen. Und dann fiel mir plötzlich auf, wie einfach die Auswertung sein kann, und dabei dennoch extrem gute Wert liefern:
- Für die (unbekannte) Folge von Byte-Werten schlagen wir für jede Werte-Änderung die zugehörige Wahrscheinlichkeit aus den obigen Analyse-Daten nach.
- Die einzelnen Wahrscheinlichkeiten werden aufsummiert und am Ende durch die Zahl der Werte geteilt (Mittelwert).
- Durch eine Normalisierung des Ergebnisses mit dem Mittelwert der Wahrscheinlichkeiten der statistischen Daten muss man bei der Bewertung nicht mit "Magic Numbers" hantieren, sondern kann im Wertebereich bis 1.0 eine prozentuale Wahrscheinlichkeit ablesen, die angibt, wie wahrscheinlich die Byte-Folge Text enthält.
Die Ergebnisse waren schon sehr ordentlich, aber um die Lage noch eindeutiger zu darzustellen, habe ich mich noch für ein "Penalty"-Verfahren entschieden: trifft man bei der Analyse der unbekannten Byte-Folge auf einen Übergang, der in der Datenbasis überhaupt nicht vorhanden ist, wird (statt dem eigentlichen Wert 0) ein Strafwert von -1.0 eingerechnet. Den habe ich willkürlich gewählt. Da das Maximum, das pro Übergang hinzukommen kann, 1.0 ist, nahm ich einfach den zugehörigen negativen Wert.
Anders formuliert: wenn ich auf ein Byte-Paar treffe, das in meinen 12000 C#-Dateien, die ich zunächst analysiert hatte, niemals vorkommt, dann gehe ich stark davon aus, dass es sich beim aktuellen Beispiel nicht um C#-Text handelt und bestrafe das entsprechend. Natürlich besteht immer die Wahrscheinlichkeit, dass es sich um eine legitime, aber sehr seltene Situation handelt, oder dass in der Datenbasis für den Lernprozess etwas falsch war oder gefehlt hat. In der Praxis aber sollte das für zu prüfenden C#-Text sehr selten vorkommen – für andere Daten, insbesondere Binärdaten, aber sehr häufig.
Die Implementierung sieht also etwa so aus, wobei "_probabilities" hier die normalisierten Wahrscheinlichkeiten wie oben gezeigt sind, "_meanProbability" der Mittelwert daraus (also ebenfalls 0 <= _meanProbability <= 1):
public double Analyze(byte[] rawData)
{
if (rawData == null || rawData.Length < 2)
{
return 0.0;
}
var sum = 0.0;
for (var n = 0; n < rawData.Length - 1; n++)
{
var current = rawData[n];
var next = rawData[n + 1];
var probability = _probabilities[current, next];
if (probability <= double.Epsilon)
{
sum -= 1.0; // penalty
}
else
{
sum += probability;
}
}
var result = sum/rawData.Length;
var normalizedResult = Math.Min(1.0, result/_meanProbability);
return normalizedResult;
}
Bei der Normalisierung habe ich im Beispiel bewusst darauf verzichtet, den unteren Wert zu begrenzen, damit ich mit ein paar Beispielwerten demonstrieren kann, wie eindeutig die Unterscheidung verschiedener Daten damit ist.
Zum Testen des Algorithmus habe ich verschiedenste Dateien verwendet. Die C#-Dateien entstammten dabei natürlich nicht dem ursprünglichen Pool der Lerndaten. Dennoch war das Ergebnis immer 1.0. Das heißt, die Auswertung hat zuverlässig erkannt, dass unbekannte C#-Dateien mit extrem hoher Wahrscheinlichkeit aus Text bestehen :-). Interessanter ist natürlich, was passiert, wenn man Binärdaten einspeist. Hier das Ergebnis für einige Beispiele:
C#-Datei = 1
ZIP-Archiv = -37,4332437827092
DLL = -22,5056453228032
PNG-Datei = -38,2415297674875
MP3-Datei = -37,8333106675966
AVI-Datei = -37,9571341409469
Wie man sieht, ist das Ergebnis eindeutig, und willkürlich ausgewählte Binärdateien werden zuverlässig als Nicht-Text erkannt.
Spannend war für mich nun, wie es mit anderen Text-Formaten aussieht. In der Praxis würde man für eine Allgemeingültigkeit natürlich für das Training bunt gemischte Text-Dateien auswählen. Ich habe mich aber gezielt auf C#-Dateien gestürzt. Was also passiert, wenn ich nun andere Text-Dateien verwende?
C#-Datei = 1
XML-Datei = 1
HTML-Datei = 1
Visual Basic.NET-Datei = 1
TXT-Datei = 1
RTF-Datei = 0,81447098477732
Alle möglichen Formate werden, trotz einseitiger Datenbasis, zuverlässig als Text erkannt. Lediglich die RTF-Datei ist ein Ausreißer, weil das Format wirklich sehr speziell ist. Aber selbst dafür lag die berechnete Wahrscheinlichkeit noch bei über 80%. Problematisch wurde es erst, als ich Dateien mit eingebettenen Bildern (Base64-kodiert) verwendete. Dann sank die Wahrscheinlichkeit irgendwann auf 0 ab (wenn auch mit weit geringerer Unterschreitung als bei den tatsächlichen Binärdaten; das Minimum der geprüften Dateien lag etwa bei -1,7). Als Gegenprobe habe ich in die Analyse auch RTF-Dateien mit aufgenommen, wodurch die Wahrscheinlichkeit für diese (auch mit eingebetteten Bildern) sofort ebenfalls auf glatte 1.0 hochschnellte.
Hinweis: es ist nicht nötig, zur Auswertung jeweils die gesamte Datei durchzuprüfen, wie es im Beispiel-Code oben gemacht wird. Ich habe sehr zuverlässige und vergleichbar eindeutige Ergebnisse auch dann erhalten, wenn ich nur die ersten z.B. 128 oder 256 Bytes einer Datei untersucht habe.
Insgesamt also eine schöne und erstaunlich einfache Möglichkeit, sehr zuverlässig Aussagen über die Art des Inhalts von Dateien (oder Byte-Streams) machen zu können.
Tags: Inhaltsanalyse · Markow-Kette
